Динамический диапазон анализаторов спектра: особенности оценки и учета при измерениях (Часть 1)

     Одним из главных требований, предъявляемых к радиоизмерительному оборудованию, является достоверность результатов измерений, то есть их соответствие анализируемым физическим процессам. При этом грань между достоверностью и недостоверностью может быть как весьма резкой, как это свойственно, например, стрелочным приборам, так и незаметной, и в последнем случае требуется установить ее четкие критерии. Помимо базовых условий эксплуатации любых радиоизмерительных приборов, в том числе и анализаторов спектра, для со хранения достоверности результатов измерений необходимо, чтобы уровень входного сигнала лежал в некотором интервале, который принято называть динамическим диапазоном [2, 3].

   Динамический диапазон (ДД, англ. Dynamic Range, DR) является одной из ключевых характеристик АС и характеризует их способность одновременно обрабатывать сигналы, существенно различающиеся по мощности. Случаи таких измерений встречаются:

• в радиолокации, где оцениваются характеристики излученного и отраженного сигналов;
• в системах радиосвязи с временным разделением восходящего и нисходящего каналов (4G, 5G);
• в системах спутниковой и закрытой радиосвязи;
• в технических средствах обнаружения и защиты от утечки информации по каналам, связанным с побочными электромагнитными излучениями и наводками.

   Учитывая важность не столько понятия ДД, сколько получения правильных результатов измерений в упомянутых приложениях АС, рассмотрим суть и особенности учета и экспериментального определения динамического диапазона. При этом следует помнить, что его значение обычно не указывается в эксплуатационной документации, поскольку существенно зависит от характера измерений и настроек АС.

ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ДИНАМИЧЕСКИЙ ДИАПАЗОН АС

   В АС линейная часть работает по аналогии с обычными радиоприемниками, с переносом по частоте. Нижняя граница ДД определяется совокупностью собственного теплового шума и фазового шума гетеродинов. Верхняя граница может устанавливаться либо точкой компрессии 1 дБ, либо уровнем интермодуляционных продуктов, возникающих при перегрузке линейной части АС и проявляющихся на отображаемой спектрограмме. Собственно говоря, это и есть критерии для определения допустимых границ входного сигнала для АС при условии сохранения достоверности результатов измерений. Исходя из этого, очевидно, что при произвольных настройках ДД нельзя приравнивать к диапазону отображения. Действительно, при уровнях сигнала, близких к максимально допустимому значению, используется дополнительное ослабление, которое повышает уровень отображаемого шума. В свою очередь, минимальный уровень шума будет достигнут, когда ослабление встроенного аттенюатора минимально и в идеале равно нулю, но этот режим ухудшает условия согласования АС по входу с подключаемым оборудованием. Для снижения уровня отображаемого шума в режиме минимального ослабления целесообразно использовать встроенный предварительный усилитель АС, который также способен ухудшать согласование и несколько увеличивать амплитудную погрешность.

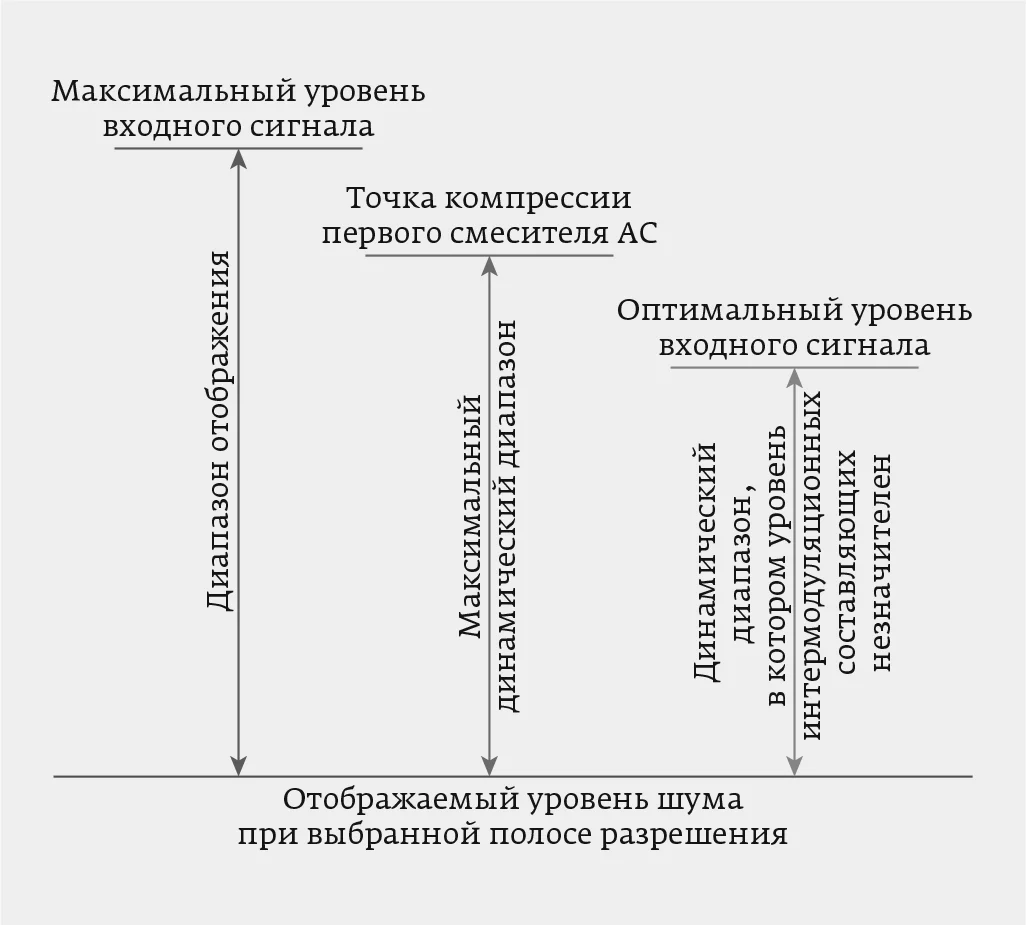
	Рис. 1. Качественное соотношение диапазона отображения, максимального динамического диапазона и динамического диапазона, в котором уровень гармоник и продуктов интермодуляции незначителен

    Верхняя граница максимального ДД лежит ниже предельного отображаемого уровня сигналов и определяется точкой компрессии 1 дБ (рис. 1), однако при этом возникает семейство отображаемых спектральных составляющих весьма существенного уровня и не имеющих никакого отношения к структуре спектра измеряемого сигнала, в том числе и при работе с небольшой полосой обзора. В результате этого такие спектрограммы лишаются достоверности, что недопустимо. Ситуация еще более ухудшится, если АС реализует два или три переноса по частоте. Ввиду этого в современных АС предусматриваются ограничения опорного уровня, который при выбранном ослаблении входного аттенюатора должен оставаться существенно ниже точки компрессии 1 дБ.

   Из изложенного следует важный вывод о том, что максимальный динамический диапазон может быть реализован лишь в очень узком круге измерений, когда формирование интермодуляционных составляющих значительного уровня невозможно. В частности, это случаи измерения моногармонических сигналов и фазовых шумов на значительном удалении от несущей.

   Интермодуляционные и гармонические составляющие являются нежелательными продуктами работы линейного тракта АС. Ввиду этого наиболее качественные результаты измерений будут соответствовать случаю, когда они являются пренебрежимо малыми, что соответствует невысокому уровню сигнала на смесителе. Но снижение последнего приводит к ухудшению отношения «сигнал – шум», что может не позволить провести некоторые виды измерений, например, на соответствие радиосигналов установленной спектральной маске. Ограничение ДД сверху, вызванное интермодуляционными или гармоническими составляющими, в общем случае достигается при разных уровнях входного сигнала, следовательно, оно будет характеризовать разные значения ДД. При этом критерий определения достижения входным сигналом предельного уровня состоит в равенстве указанных составляющих уровню шума, что соответствует максимуму ДД, свободного от продуктов интермодуляции. Таким образом, значение ДД меняется при изменении уровня сигнала на входе АС и должно иметь экстремум.

   Исходя из этих качественных соображений, могут быть произведены расчеты ДД с учетом описанных ограничивающих факторов [4].

СОБСТВЕННЫЕ ШУМЫ ЛИНЕЙНОГО ТРАКТА И ИНТЕРМОДУЛЯЦИОННЫЕ ПРОДУКТЫ

   Будем считать, что на вход АС поступает сигнал с поло сой, существенно большей полосы пропускания фильтра промежуточной частоты Δf. Внутренние шумы АС, как и для любого высокочувствительного приемного устройства, определяются первым усилителем в линей ном тракте и характеризуются шум-фактором NF, который показывает приращение шума относительно уровня, обусловленного тепловыми процессами и для входного со противления тракта 50 Ом составляющего L_T = –174 дБмВт в полосе 1 Гц. Учитывая свойства теплового шума, его уровень L_NR относительно уровня сигнала на входе смесителя L_S составит

L_NR = L_N – L_S = L_T + 10 lg(Δf_Ш) + NF – L_S,    (1)

где Δf_Ш – шумовая полоса фильтра, Гц; L_N – абсолютный уровень шума. Шум-фактор измеряется в дБ, все абсолютные мощности – в дБмВт. Формула (1) не учитывает тип детектора и усреднение за счет использования видеофильтра. Как отмечается в [4], при использовании детектора выборки и усреднения узкополосным видеофильтром расчетное значение L_NR следует увеличить на 2,5 дБ из-за недооценки уровня шума.

   Для анализатора спектра уравнение для расчета относительного уровня интермодуляционных составляющих порядка n имеет вид L_IMnR = –(n – 1)(IPn_in – LS), где IPn_in – входная мощность, дБмВт, соответствующая точке пересечения порядка n. При больших уровнях сигнала наибольшее влияние на результаты измерений оказывают продукты интермодуляции третьего порядка, откуда имеем

L_IM3R = –2(IP3_in – L_S).   (2)

   Менее эффективный процесс формирования составляющих второго порядка приводит к формированию гармоник с относительным уровнем [4]

L_2R = –(SHI_in – LS),   (3)

где SHI_in — мощность, соответствующая точке пересечения второго порядка, дБмВт, приведенная ко входу АС. Использование относительных уровней продуктов интермодуляции в расчетах позволяет уйти от учета ослабления, установленного на аттенюаторе АС. При этом в формулы (2) и (3) следует подставлять значения IP3_in и SHI_in, соответствующие входу АС, то есть первому смесителю и нулевому ослаблению аттенюатора.

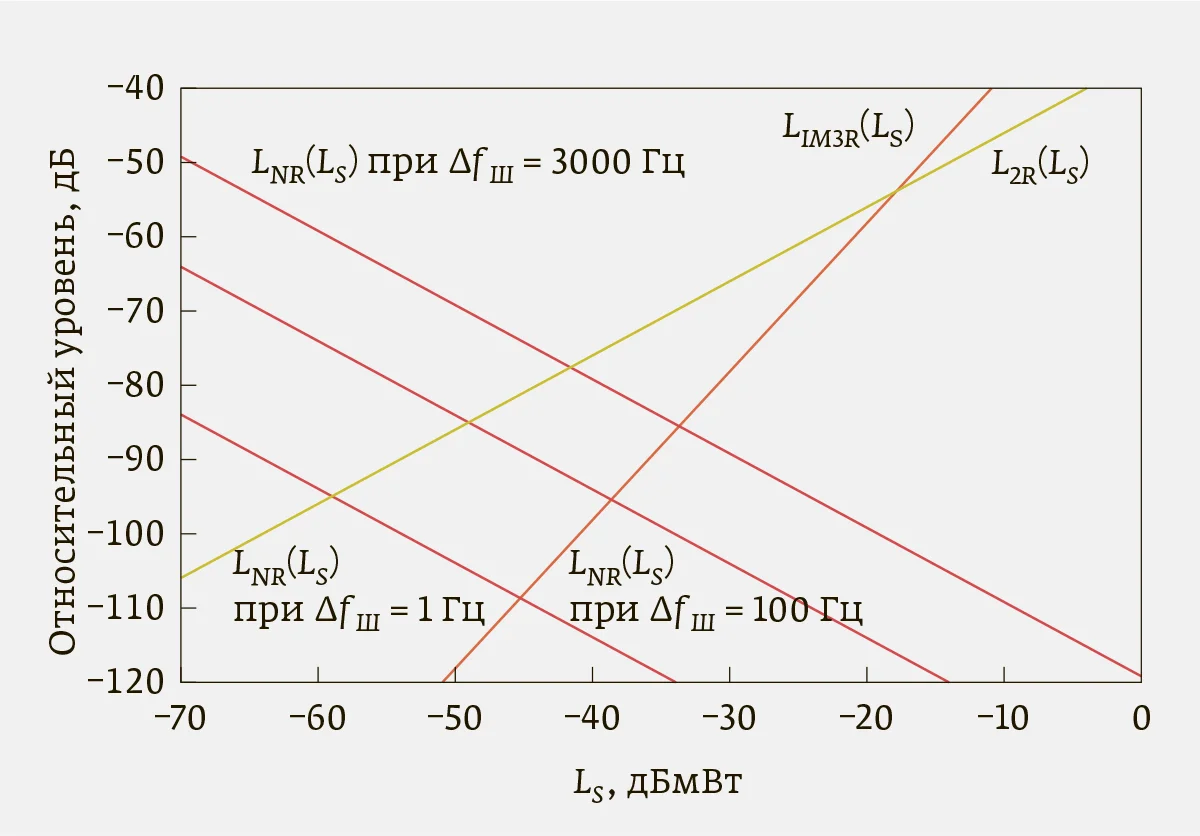
	Рис. 2. Графики функций LNR(LS), LIM3R(LS), L2R(LS) для выбранных шумовых полос

   На рис. 2 представлены графики линейных функций L_NR (L_S) для Δf_Ш = 1; 100; 3000 Гц, а также зависимостей LIM_3R (L_S) и L_2R (L_S). Графики построены для IP3_in = 9 дБмВт и SHI_in = 36 дБмВт. Увеличение уровня сигнала на смесителе приводит к уменьшению относительного уровня шума линейного тракта АС и одновременно повышает интермодуляционные составляющие со скоростью 3 или 2 дБ/дБ. Ввиду этого за характеристику ДД можно принять минимальный модуль значений LIM_3R (L_S) (или L_2R (L_S)) и L_NR (L_S).

   В зависимости от сути проводимых измерений интермодуляционные спектральные составляющие могут ограничивать ДД сверху. В таких случаях целесообразно выбирать оптимальный уровень сигнала на входе смесителя, соответствующий для выбранной полосы разрешения точке пересечения прямых L_NR (L_S) и L_IM3R (L_S) (или L_2R (L_S)), в которой уравниваются уровни шума и продуктов ин термодуляции. В представленном на рис. 2 примере это достигается для полосы 100 Гц при L_S = –38,5 дБмВт, когда относительный уровень собственных шумов равен –95 дБ. Соответственно, при этом уровень интермодуляционных составляющих и уровень шума линейного тракта равны –135,5 дБмВт.

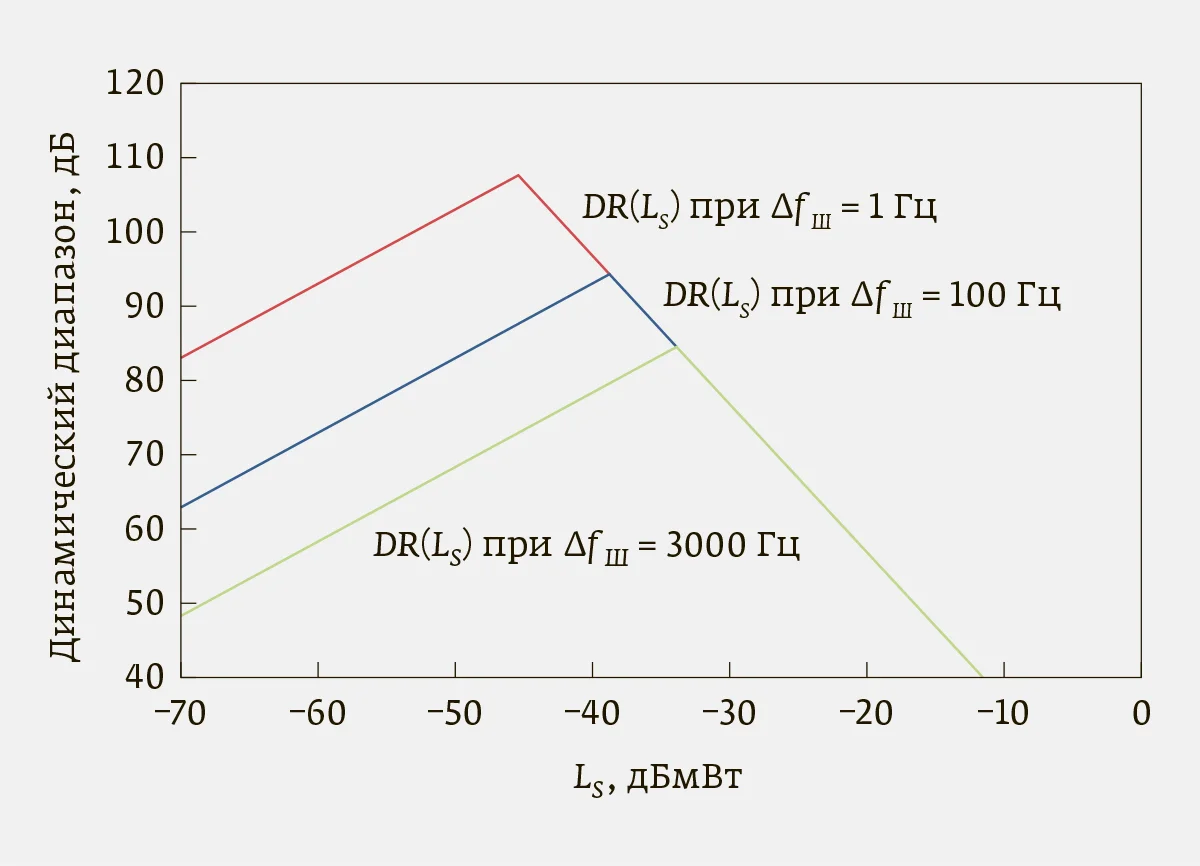
	Рис. 3. Графики функций DR(LS) для выбранных шумовых полос

   Учитывая, что интермодуляционные составляющие третьего порядка проявляются при более низких уровнях входного сигнала, далее будем ориентироваться на них. Важно подчеркнуть, что с учетом особенности работы АС под ДД следует понимать максимально возможное изменение уровня сигнала на смесителе относительно его текущего уровня до ограничения либо собственными шумами, либо продуктами нелинейности. Исходя из такого определения, на рис. 3 для тех же шумовых полос построены графики D_R (L_S), отражающие зависимость динамического диапазона от уровня сигнала на первом смесителе и имеющие по одной точке, соответствующей оптимальному значению L_S. Как видно из представленных графиков, увеличение полосы всегда приводит к снижению максимального доступного ДД. Однако во многих приложениях про водить измерения с малой полосой разрешения невозможно, и тогда, в особенности для широкополосных сигналов, максимум ДД может быть ограничен значением 20–35 дБ.

   Представленные рассуждения позволяют выдвинуть требования к качеству линейного тракта АС, которые, очевидно, состоят в максимально возможной линейности и минимально возможных шумах (min(NF), max(IP3_in), max(SHI_in))

РАСЧЕТ ОПТИМАЛЬНОГО УРОВНЯ СИГНАЛА НА ВХОДЕ СМЕСИТЕЛЯ АС И МАКСИМАЛЬНОГО ЗНАЧЕНИЯ ДД

   Как было определено выше, оптимальный уровень сигнала L_S,onm соответствует равенству интермодуляционных и шумовых компонент в спектре. Его можно получить по парным приравниванием (1) и (2), (1) и (3), что дает следующие уравнения:

–174 дБмВт + 10 lg(Δf_Ш) + NF – L_S = –2(IP3_in – L_S );

–174 дБмВт + 10 lg(Δf_Ш) + NF – L_S = –(SHI_in – L_S ).   (4)

   Их решение относительно L_S позволяет рассчитать оптимальные значения уровня сигнала на смесителе. Для составляющих третьего порядка он составит 

L_S,onm = (2IP3in–174 дБмВт + 10 lg(ΔfШ ) + NF)/3,   (5) 

для составляющих второго порядка

L_S,onm = (SHI_in – 174 дБмВт + 10 lg(Δf_Ш ) + NF)/2.   (6)

   При L_S = L_S,onm максимальный динамический диапазон DRmax будет соответствовать разнице между значениями L_S и L_N либо –L_IM3R (или –L_2R ). Отсюда можно получить, что с учетом (5) для составляющих третьего порядка

DR_max = L_S,onm– L_N = –L_IM3R = = 2(IP3_in + 174 дБмВт – 10 lg(Δf_Ш ) – NF)/3,   (7) 

с учетом (6) для составляющих второго порядка 

DR_max = L_S,onm– L_N = –L_2R = = (SHI_in + 174 дБмВт – 10 lg(Δf_Ш ) – NF)/2.   (8) 

   Из уравнений (7) и (8) следует, что для получения максимально возможного ДД в точке равенства собственно го шума и продуктов интермодуляции следует использовать максимально линейный тракт с минимально возможным шумом. Для сравнения АС в этой части удобно использовать показатель качества Q = IP3_in – NF. Для высококачественных АС, имеющих IP3_in ~ 15 дБмВт, NF ~ 15 дБ, значение Q близко к 0 дБмВт. В инженерной практике для быстрой оценки макси мального динамического диапазона целесообразно использовать формулы, аналогичные (7) и (8), но включающие в себя отображаемый уровень шума L_N для вы бранной полосы и значение IP3_in или SHI_in как параметры, определяющие значение DR_max. Из (1), (7) и (8) следует, что такие формулы будут иметь вид

DR_max = 2(IP3_in – L_N )/3; DR_max = (SHI_in – LN )/2.   (9) 

   Уравнения (9) являются основой для экспериментального определения DR_max для конкретного образца АС. Приведенные соотношения относятся к уровню сиг нала на входе первого смесителя, то есть соответствуют нулевому ослаблению встроенного аттенюатора АС. Достижение максимального ДД осуществляется установкой его ослабления на значение, при котором достигается L_S ≈ L_S,onm. Лучшие в этом отношении результаты дают АС, позволяющие менять ослабление с шагом 1 дБ. В противном случае в критичных приложениях следует использовать внешние ступенчатые аттенюаторы с приемлемым шагом.

ВЛИЯНИЕ ФАЗОВОГО ШУМА ГЕТЕРОДИНОВ АС НА ДИНАМИЧЕСКИЙ ДИАПАЗОН 

   Влияние фазового шума (ФШ) на результаты измерений в АС проявляется в его переносе на входные сигналы в процессе работы смесителей. ФШ АС ограничивает снизу ДД. Кроме того, требования по минимальным ФШ для АС являются определяющими в случаях, когда необходимо отобразить очень слабые составляю щие спектра в окрестности других, имеющих большую мощность, поскольку ФШ АС может полностью скрыть первые за счет того, что при переносе на промежуточную частоту ФШ будут отображаться как шумовая модуляция в окрестности перенесенной составляющей с высоким уровнем.

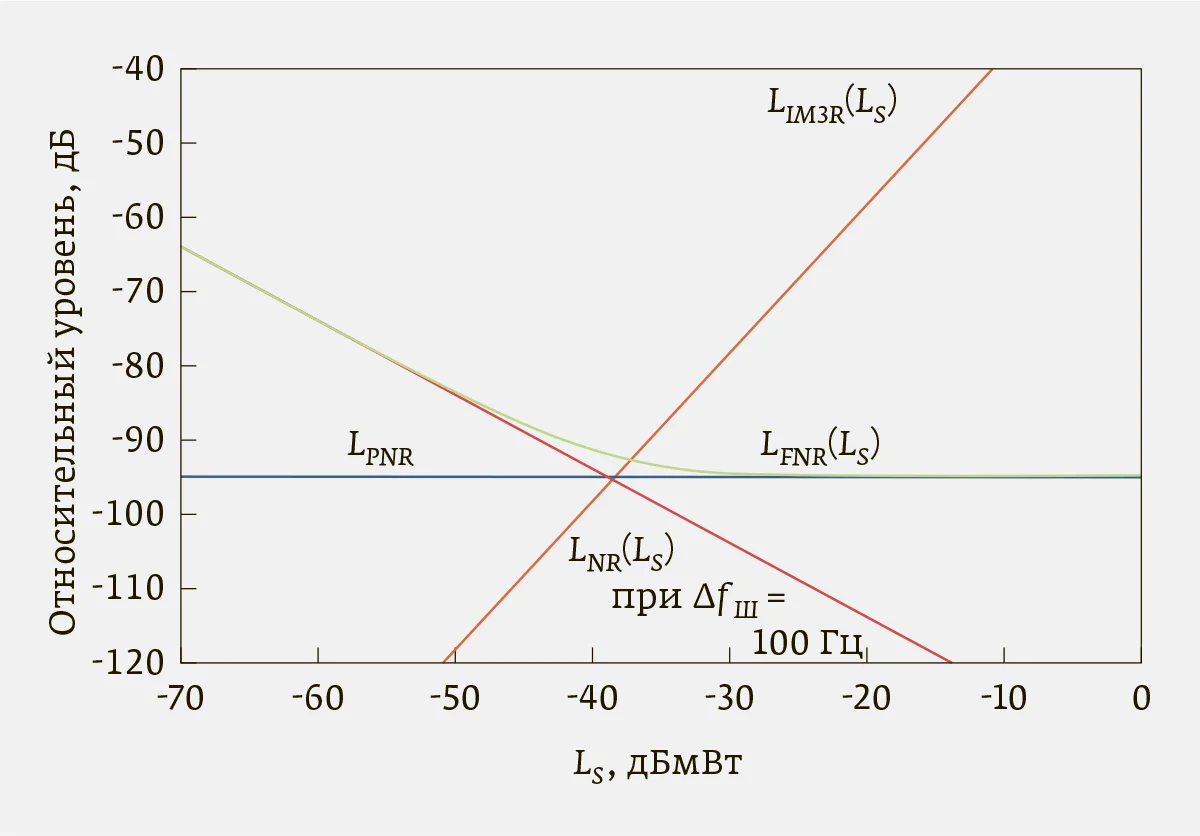
	Рис. 4. Графики функций LNR(LS), LIM3R(LS), LFNR(LS) для выбранных шумовых полос

   Ввиду особенностей обработки и переноса сигналов по частоте уровень ФШ относительно входного сигнала L_PNR не будет зависеть от его уровня. Если измерения проводятся на частотах с большей отстройкой от несущей, чем продукты интермодуляции третьего порядка, то они не влияют на результаты измерений в части ограничения ДД снизу. В то же время они, располагаясь наиболее близ ко к сигналам с большим уровнем, как и раньше, ограничивают его сверху. 

   Абсолютный уровень фазового шума L_PN (f) определяется частотной расстройкой f между сигналом гетеро дина и измеряемой частотой, а также шумовой полосой фильтра промежуточной частоты: 

L_PN (f) = L_PN1 (f)+10 lg(Δf_Ш),   (10)

где L_PN1 (f) – уровень ФШ при шумовой полосе 1 Гц. Поскольку тепловые и фазовые шумы являются некоррелированными, то они складываются друг с другом линейно. 

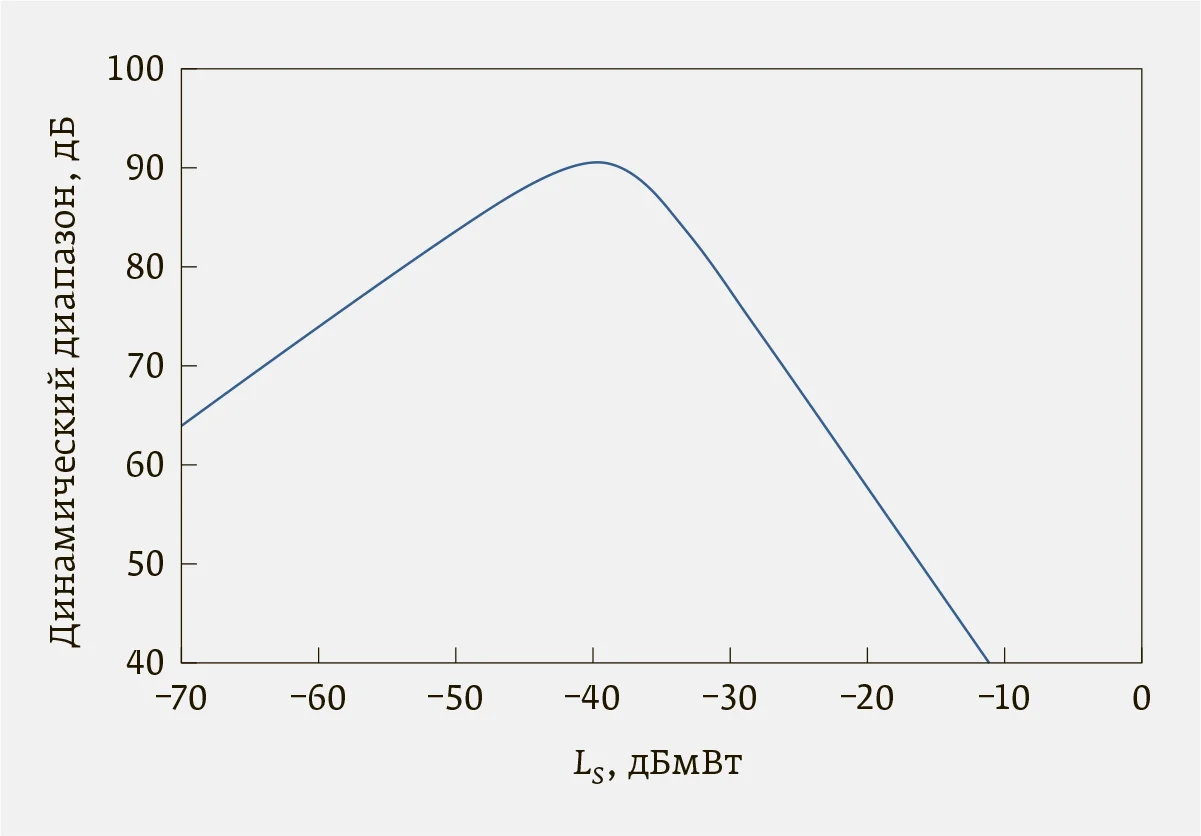
	Рис. 5. Зависимость DR(LS), построенная для ΔfШ = 100 Гц

   На рис. 4 показаны графики функций L_NR (L_S) и L_FNR (L_S), построенные для шумовой полосы Δf_Ш = 100 Гц, причем зависимость L_FNR (L_S) характеризует относительный уровень полного суммарного шума тракта АС. Также на рис. 4 показана зависимость L_IM3R (L_S). Все графики построены для тех же характеристик АС, какие использовались выше, значение L_PN1 принято равным –115 дБн. Как видно, наличие ФШ повышает совокупный шум, несколько смещая значение L_S,onm в сторону меньших значений, а также снижая максимальный ДД. На рис. 5 представлена зависимость DR(L_S), учитывающая тепловой и фазовый шумы АС, а также нелинейность тракта в части продуктов интермодуляции третьего порядка. Сопоставление зависимостей DR(L_S) на рис. 3 и 5 показывает снижение максимального ДД с 94,1 дБ до 90,6 дБ и смещение L_S,onm с –38,6 дБмВт на –39,7 дБмВт. Следовательно, при строгом поиске оптимума настроек АС в целях максимизации ДД учет фазового шума является обязательным.

   Таким образом, при расчете значения ДД следует учитывать и ФШ в случае измерения слабых сигналов либо их фазовых шумов в окрестности составляющих существенного уровня. Наличие ФШ несколько снижает максимальный ДД, что может быть важным, например, при оценке точек пересечения нечетных порядков для АС и при измерениях фазовых шумов генераторов несущей. 

ЛИТЕРАТУРА 

1. Ратхор Т.С. Цифровые измерения. АЦП/ЦАП. М.: ТЕХНОСФЕРА, 2006. 392 с. 

2. Радиотехника. Энциклопедия // Под ред. Мазора Ю.Л., Мачусского Е.А., Правды В.И. М., 2016. 944 с. 

3. Ширман Я.Д., Багдасарян С.Т., Маляренко А.С. и др. Радиоэлектронные системы. Основы построения и теория // Под ред. Ширмана Я.Д. М.: Радиотехника, 2007. 512 с. 

4. Раушер К. Основы спектрального анализа. М.: R&S, Горячая линия – Телеком, 2006. 226 с